小乖乖的妙妙屋
0%

发表于 更新于 分类于
本文字数： 11k 阅读时长 ≈ 19 分钟

文章目录:

  1. 环境配置与 "hello OS！"

  2. 从实模式到保护模式

1 环境配置与 "hello OS！"

前言

上的是武大网安院严老师的课头。使用的教材是 Orange's 啥啥的那本书。因为第一次课配环境血压飙的有点快，所以开个帖来记录实验过程。

文章里包含大量指向有用文档的超链接，但是都是夹在文字中的，长这样（不用点，只是演示一下长什么样）。看起来不明显，需要仔细识别。后续可能会考虑改进一下，把链接摆在明显的位置，或是换一个主题。

本人的博客向来是话比较多的，因为个人倾向于把所有想到的东西全部写进来。望多多包涵。

随课持续更新中。也可能开一篇新的文章。

说起来，我对这篇博客的定位其实不是特别的明朗。我并不清楚自己到底想写出一篇什么样的东西来。

事实上，如果只是想记录实验步骤和课后习题什么的答案，去年已经有大佬写过了，而且人家的可读性、排版、完成度等也要远远优于我。

因此，我可能更倾向于把我的文章定位为比较随性的、实验过程中发现的有趣的、试图详细理解研究的问题的记录随笔。

因为比较笨，所以我写 acm 题解时大多数时候会默认读者和我一样笨，然后把整个思考过程的过程都很啰嗦地写出来。我暑假语雀更了上万字，不过群友似乎不怎么看得下去。其实说白了，就是我不太擅长整理和精炼语言。

这个不太好的习惯被我延续到了 OS 实验的博客里。因此这对于只打算看个结果自己想和参考下操作的朋友不是特别的友好。我会在更新的过程中慢慢改进的。

1.1 虚拟机平台与操作系统选择

1.1.1 操作系统

根据老师的说法，64 位系统编译 32 位程序比较麻烦，而且有些东西不一样，折腾起来可能很麻烦，所以建议使用 32 位的操作系统。Ubuntu 版本中带有 i386 的，就是 32 位的。

可以在清华源下载想要的系统光驱。16 往前的才有 i386。也可以去别的地方，无所谓。

我使用的是 ubuntu-16.04.6-desktop-i386。下个 torrent 文件用迅雷下就行，蛮快的。

1.1.2 虚拟机平台

关于虚拟机平台，老师推荐 Virtual Box，因为它开源免费，当然它 bug 也很多；VMware 也是推荐选项，它更稳定，不过大多数都是盗版，不排除出现一些难以解决的问题。老师不推荐我们使用 wsl。wsl 确实蛋疼，没有 service 也没有 systemctl，之前装 mysql 研究了半天才找到怎么开启服务。

周围有好多大佬用的奇奇怪怪的非 desktop 的 linux，看着好帅，我比较菜，就算了吧。

我相对熟悉的是 VMware。当然我也试了一下 Virtual Box，但是折腾半天虚拟机一直卡在启动页面打不开，就不想用了。

1.2 一些"无关紧要"的前置准备

1.2.1 修改软件源到镜像站

之前做过很多次的事情。这里我修改的是清华源，参考这里。

1
2
3
4
5
6
7
# 先备份一下
cp /etc/apt/sources.list ~/sources.list
# 修改来源 把文档里的内容复制进去（记得改版本）
# 你也可以用 vi，但是用起来很怪，可能是我误触了什么，以后再下个 vim 吧
sudo gedit ~/sources.list
# 然后重新 update 一下
sudo apt update

注意，如果在 sudo apt update 后提示安全证书问题，你可以把 sources.list 里的 https 全部改成 http。

1.2.2 安装 VMware tools 与设置共享文件夹

这里只记录下我具体做了什么，因为我也不知道我在干什么。我用的是 VMware® Workstation 16 Pro。怎么搞到的就不说了。

我先设置的是共享文件夹。在 "虚拟机 -> 设置 -> 选项 -> 共享文件夹"。改成永久启用，然后添加主机上的一个路径。确认之后，类似 wsl2，你就可以通过 /mnt/hgfs 访问主机上的这个文件夹了。

理论上讲这一步最好是重装完 tools 再来做的，但是我提前做了，不清楚会不会有什么影响，所以我将其记录下来作为参考。

但此时我还是不能共享剪切板。所以我重启了一下，然后在菜单栏的虚拟机选项卡里的 "重新安装 VMware tools" 就变黑了。点一下，它大概会把那些东西以一个虚拟光盘的样子挂给你。（因为路径显示的是 /mnt/xxx，所以我猜是挂载的什么玩意）

然后把中间那个 tar.gz 格式的文件复制到 home 目录下，解压出来。不建议直接在那个目录下解压，一个是没有权限，一个是我不知道会发生什么，也不排除本来就是只读的。

然后在解压出来的 VMware-tools-distrib 里打开 terminal，运行 sudo ./vmware-install.pl。

然后我就全程回车保持默认，反正也看不懂。

注意，重装过程中的所有 overwrite 选项都是默认 no，个人是建议全部输入 yes。

然后就好了，然后就可以共享剪切板了。声明一下：如果你还没好，我也不太懂，因为我确实不知道这个安装程序是在干什么。

重装了 tools 后，原来设置的共享文件夹找不到了。所以你需要再删掉重新添加一次。用不用重启我忘了。

我装完 VM tools 之后 VMware 偶尔会出现半分钟左右的莫名奇妙的无响应，不知道在加载什么东西。且这段时间里我主机无法使用复制黏贴功能。不知道有没有遇到相同问题的大佬指导一下。我用的是 VMware® Workstation 16 Pro 16.1.2 build-17966106。

1.2.3 为 github 账户添加新的 ssh key

我有三个虚拟机和一个主机，所以我的 github 账户有四个 key。

当然这个只是个人习惯，完全没打算用远端仓库或是习惯直接输入账号密码的可以无视这部分。

需要注意的是，出于安全上的考虑，过去很多教程里生成 key 的方式不再被支持了。

可以参考官方的指南。

因为我 ssh 用的不多，基本上是每个机子只用同一个 key 到处连，所以没有管 ssh-agent。生成完直接看下一节的添加就行。

也可以参考这个博客。too much 教程，这里就不扯皮了。

1.2.4 zsh oh-my-zsh 相关配置

老师说你们别折腾什么中文输入法，说有人折腾了半天结果把系统搞崩了，最后重装虚拟机。中文输入法确实没有必要，但是 zsh 和 oh-my-zsh 必须要有！（暴论

好吧这个依然是个人习惯。

首先是安装 zsh，很简单 sudo apt install zsh。

问题在于怎么设置 zsh 为默认终端。这个东西这个版本上不能直接 chsh -s /bin/zsh，要在 gnome terminal 的图形化界面里面手动修改。

需要注意的是它的界面和平常用的 windows 不太一样。当终端在前台运行时，桌面左上角会有一个 terminal 的字样，光标移动到它上面，才会出现我们平常见的菜单栏。Terminal -> Preferences -> Profiles，可以直接改原来的这个配置，也可以建一个新的，但是要记得改下面的 profile used when launching a new terminal。

把 profile 里 run a custom command install of my shell 勾上，写上 zsh。顺便把下面的 exit 效果设置成退出终端，体验就和 chsh 基本一致了。

然后自然是要安装 oh-my-zsh。以前小乖乖的游记的时候我用的是改 host 的方式。其实没有必要。我们可以借助国内的镜像。

我们知道这个 oh-my-zsh 是开源的。之所以直接用官网给的安装链接安装不了，是因为 raw.github.com 上不去。那我们直接把这个文件下载下来不久行了。

当然我是连 github 本身也上不去的，所以我选择的是直接使用 gitee 上的镜像。

首先把 /tools/install.sh 搞下来。直接 clone 整个项目或是 wget 之类的都行。

然后打开来看一眼，它告诉你可以执行的时候加上 REMOTE 参数来指定源。指定源来跑就行了。我用的是 ssh，用 http 也一样

1
2
3
4
5
6
7
8
9
10
# You can tweak the install behavior by setting variables when running the script. For
# example, to change the path to the Oh My Zsh repository:
#   ZSH=~/.zsh sh install.sh
#
# Respects the following environment variables:
#   ZSH     - path to the Oh My Zsh repository folder (default: $HOME/.oh-my-zsh)
#   REPO    - name of the GitHub repo to install from (default: ohmyzsh/ohmyzsh)
#   REMOTE  - full remote URL of the git repo to install (default: GitHub via HTTPS)
#   BRANCH  - branch to check out immediately after install (default: master)
REMOTE=git@gitee.com:mirrors/oh-my-zsh.git sh install.sh

弄完后，可以尝试添加一些插件。比如 zsh-syntax-highlighting。

照着它的文档弄就行了。我们装了 ohmyzsh，所以按它教的 ohmyzsh 安装插件的方式来装。

1.3 实验环境配置

1.3.1 Bochs 安装

Bochs 是个模拟器。教材用的是 Bochs，我也不会 Qemu，所以这里用 Bochs。后续可能会考虑看一下 Qemu。

P.S. 模拟器和虚拟机是有很大区别的。模拟器的所有指令都需要经过软件的模拟，也因此它可以跑另一种 CPU 架构下的系统。而个人理解的虚拟化强调的是物理资源的抽象和分配。具体的可以百度 Formal Requirements for Virtualizable Third Generation Architectures 这篇论文了解。当然这和这个实验没有任何关系，我们并不是在研究虚拟化技术，我们研究的是如何实现一个简单的操作系统。

Bochs 可以从官方网站上下载。似乎需要翻墙，各显神通吧。但是我自己在尝试下载的时候，找了半天下载入口。

其实你需要点 Get Bochs -> see all release，然后会跳转到这里。在这里下载 tar.gz 格式的安装包。用共享文件夹或是别的手段搞到虚拟机里。因为我们后续需要使用一些特殊的 configure 选项，所以要下载源码手动编译。

编译的过程可以参考官方文档，上面也写有各个参数的详细意义。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 安装依赖。虽然说 make 的时候再根据报错来装也可以。
sudo apt install build-essential \
    libx11-dev \
    libxrandr-dev \
    libsdl1.2-dev \
    vgabios \
    bximage
# 运行 configure 脚本 带上 PPT 上要求的参数
# 第一个参数好像是 display library 相关的 
# 第二个是开启 debug
# 最后这个参数我的版本似乎不需要加 会被直接忽略
./configure --with-sdl --enable-debugger --enable-disasm
# 编译和安装
make
sudo make install

P.S. 安装完成后，根据文档的 3.4.1.3，文件的默认目录是 /usr/local/xxx。在后续修改 bochsrc 时会用到 /usr/local/share/bochs 这个目录。

1.3.2 nasm 安装

本实验使用 nasm 来编译汇编源码。直接 sudo apt install nasm 即可。

1.4 Hello OS!

1.4.1 随书源码下载

这本书是由随书源码的。osfs00是这些源码的总目录和随书光碟。课上到哪就去对应的链接里找源码，比如这一节的。老师也会下载了丢在群里，可以用共享文件夹传到虚拟机里。

可以 clone 下来后修改下 boshsrc 直接 make，因为它有一个写好的 makefile。下面我们不用它的 makefile，一步一步手动进行，先熟悉一下。

1.4.2 我们要做什么？

计算机加电时，首先执行的是 BIOS。这是集成在硬件（芯片）中的程序，它会完成基本的 IO 初始化和硬件自检，然后运行系统引导程序，将 OS 装载到 ram 中，并将计算机控制权交给 OS。

或者我们可以说，它的功能是：初始化硬件平台和提供硬件的软件抽象，引导操作系统启动。

我们接下来实现的，其实是操作系统的一个部分：一个引导程序（OS Boot Loader）。在平时，boot loader 的功能是将 OS kernel 装载到内存中。但是我们现在还搞不出内核这种复杂的东西。

因此，在本次实验中，我们其实是利用 Boot Loader 来跑一段简单的汇编程序。在这个过程中体验 PC 机启动和操作系统的初始化过程。

1.4.3 制作一张空白软盘

首先我们需要一张空白的虚拟软盘。Bochs 为我们提供了一个方便的虚拟光驱创建工具 bximage。相关的参数等可以在这里查到。

直接运行 bximage，会有一个交互界面。根据提示一步一步进行就行了。我们需要的是一个软盘(fd, floppy image)，其余部分可以全部保持默认。你也可以改名字。

创建完成后，它会有提示，比如：The following line should appear in your bochsrc: floppya: image="b.img", status=inserted。

后面修改 bochsrc 的时候要用到。

根据文档，你也可以直接用指令生成这个软盘而不是进入交互界面：（从 xygg 的实验报告里 copy 出来的）

1
bximage -func=create -fd=1.44M -q a.img

当然你也可以不自己生成，直接从随书源码里的 a.img.gz 解压出来。

1.4.4 写入引导程序

引导软盘上装载的是引导程序，重点在程序。在本实验中，是由一段神奇短小的汇编代码实现的，那段代码我们后面再来分析。这里先拿随书源码中现成的 boot.asm，来制作一张引导软盘。

首先编译 nasm boot.asm -o boot.bin。

然后运行下面的指令：dd if=boot.bin of=a.img bs=512 count=1 conv=notrunc。

dd 是 linux 中自带的指令，一般用于文件的复制、读写、转码等，它可以加入很多的参数。

在这个指令中，if 和 of 指定的是输入文件和输出文件，不指定时默认是标准输出。bs 是块的大小，count 是块的数量。notrunc 的意思是 no truncate，非截断。我们这里需要的是一个完整的软盘，自然是不能让它截断的。

（虽然其实这个实验里，后面的部分并不会用上，截断了也不是不能跑）

P.S. 什么是截断？举例而言：echo "hello" > a.txt，如果 a.txt 本来是个很大的文件，那它的大小会被改变，只剩 "hello" 占的大小（当然实际可能是一个块的大小，这里只是举个例子）。截断的意思大概是，把大于输入的部分全部"删掉"，把输出文件"截"剩下输入的大小。

总之，现在我们就得到了一张引导盘。可以开始准备跑起来了。

1.4.4 boshsrc 修改

由于教材比较古老，所以随书源码的 boshsrc 有些配置已经失效了，需要进行修改。

最重要的是 romimage 和 vgaromimage 的文件目录。

最简单的判断路径对不对的方法是直接 cd 进去看看有没有这个文件。

这里的 romimage 指的是 BIOS 的 image，是随 bochs 分发的。根据文档，它的默认位置应该是：/usr/local/share/bochs/BIOS-bochs-latest。

事实上这个文件也是部署的时候从你下载的源码包里面 copy 过去的，所以你直接在你下下来的解压的文件夹里也能找到这个 image，例如 bochs-2.7/bios/BIOS-bochs-latest。

如果你实在找不到，也可以 sudo find / -name "BIOS-bochs-latest"。

至于 vgabios，直接 whereis vgabios 就可以找到（在前面安装依赖时，它是直接 apt install 的）。

软盘部分在创建后 bximage 会给出提示，我们前面提到过了。

最后面的 keyboard_mapping 部分要注释掉。这个东西 15 年就有个 issue 了。应该是个已经被抛弃的写法。

PPT 上还提到了 display_library。可以参考文档的 4.3.3。似乎与模拟器的显示有关。根据文档，不加的话默认选的应该也是 sdl（我们 configure 的参数也是 sdl），不过我还是加上了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# how much memory the emulated machine will have
megs: 32

# filename of ROM images
# 这里需要修改
romimage: file=/usr/local/share/bochs/BIOS-bochs-latest
vgaromimage: file=/usr/share/vgabios/vgabios.bin

# what disk images will be used
# 这里在创建完软盘后 bximage 会给你提示，根据提示给出的填就行
floppya: 1_44=a.img, status=inserted

# choose the boot disk.
boot: floppy

# where do we send log messages?
# log: bochsout.txt

# disable the mouse
mouse: enabled=0

# 下面的部分要注释掉
# enable key mapping, using US layout as default.
# keyboard_mapping: enabled=1, map=/usr/share/bochs/keymaps/x11-pc-us.map

# 下面的可选择加上
display_library: sdl

1.4.5 运行效果及部分常见报错

接下来就可以直接运行了 bochs -f bochsrc（也可以直接 bochs，只要在同一个目录内）。

因为前面开了 debug，所以你要在交互窗口上输入 'c'，让它继续运行。运行结果是，在弹出来的窗口上看到一行红色的 "Hello, OS world!"。

报错 1：couldn't open ROM image file。你的 bochsrc 里面路径错了需要检查一下。

报错 2：其实严格来说不是报错。如果你发现你的第一条指令不是 jmp，而是 add [bx+si],al（其实这条指令的机器码是0000）（我们开了 debug，在输入 c 的时候会注意到的），之类的很奇怪的指令，还一直报奇怪的数学运算错误之类的，那就是你的 rom image 选错了。那个是随 bochs 分发的 BIOS image，而不是你自己的创的 a.img。具体可以看前面 1.4.4。

1.5 hello os 源码分析与调试

1.5.1 无关紧要的前置准备

恭喜，我们运行了 hello os。但是别急，我们还要研究一下这个汇编程序在干什么。

在研究的过程中，我们可能会需要修改这个 boot.asm 来测试产生的变化。但是，我们每次修改都要走一遍上面的流程：编译 - 写入 - 运行（虽然其实只是 cv 三条指令）。我们可以写个脚本，让这个过程自动化。

你可能注意到了随书源码里的 makefile。你可以直接在上面改，也可以写个新的脚本。

其实那个 makefile 是可以直接用的，每次 make 解压一个新的 a.img 出来也是更合理的做法。当然，本实验中每次挂载进去的都是同样大小的内容，所以解不解压并没有什么影响。

草了，它给的那个 a.img.gz 里的 a.img 根本就不是一个空白软盘。它本来就是烧过的。所以你会发现直接注释掉 dw 0xaa55 它照样能跑，因为你写入 boot.bin 的方式是非截断的，原本就烧在里面的 0xaa55 并不会被你覆盖掉。

如果你不想像我下面这样直接生成一个新的软盘，应该删掉原来的 a.img.gz，自己用 bximage 弄出一个空白 a.img 后重新压缩成 a.img.gz。

1
2
3
4
# 如果已经存在 a.img 别忘了回答 yes
# 或者你也可以先 rm a.img
bximage -func=create -fd=1.44M -q a.img
gzip a.img

个人不建议一直用同一个被烧过的软盘跑，除非你保证每次都能把前面烧的内容覆盖掉。毕竟我们写入的方式是非截断的，并不会自动覆盖或重置掉后面的内容。

1
2
3
4
5
6
run :
	rm a.img
	bximage -func=create -fd=1.44M -q a.img
	nasm boot.asm -o boot.bin
	dd if=boot.bin of=a.img bs=512 count=1 conv=notrunc
	bochs

如果你有按我上面说的重新打包一个 a.img.gz，你也可以维持原本的 makefile 不变。

这样我们每次改完 asm 就可以直接 make 啦。

或把上面的指令抄到 sh 文件里，加个可执行权限。

然后还有一个有趣的小工具，xygg 找到的，nasmfmt，一个格式化汇编代码的小工具。

1.5.2 源码分析

下面就是随书自带的源码了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
	org	07c00h			; where the code will be running
	mov	ax, cs
	mov	ds, ax
	mov	es, ax
	call	DispStr			; let's display a string
	jmp	$			; and loop forever
DispStr:
	mov	ax, BootMessage
	mov	bp, ax			; ES:BP = string address
	mov	cx, 16			; CX = string length
	mov	ax, 01301h		; AH = 13,  AL = 01h
	mov	bx, 000ch		; RED/BLACK
	mov	dl, 0
	int	10h
	ret
BootMessage:		db	"Hello, OS world!"
times 	510-($-$$)	db	0	; fill zeros to make it exactly 512 bytes
dw 	0xaa55				; boot record signature

程序第一行是一条伪指令，用来告诉编译器你后面的程序是从 07c00h 开始的（因为根据 Intel 80386，引导盘上的程序会被放到内存的 07c00h 处）。这会影响编译器对后面部分需要寻址的指令的编译。如果不加的话，编译器会认为程序是从 00000h 开始的，导致有些指令翻译成机器码后不能找到正确的地址。（比如 jmp $ 和 mov ax, BootMessage）

后面我们会分析反汇编后的代码，在反汇编后这个伪指令的作用会体现的更清晰。

P.S. 我一开始以为它真的会使编译出的 bin 文件前面有 31kb 的空白，23333。事实上编译出来的只是机器码的二进制程序，这个程序具体会被塞到哪里，并不是由编译器来决定的，编译器能做的只有把汇编翻译成机器码。

根据大一下学期学的 16 位实模式下 x86 汇编知识，我们知道 cs, ds, es, ss 是四个段寄存器。其中 cs:ip 指向现在正在执行的指令地址，ss 和 sp 是栈相关的（pop 使 sp 增加，push 使之减少）。es 和 ds 被用作数据段，es:[di], ds:[si]。

当然我们知道 32 位下是不一样的，比如 ip 变成了 eip 等。这暂时不重要，我们以后会学到的。这里只需要知道它是在初始化段寄存器就行。以及我们这个代码内使用的寄存器，实际上全是 16 位及以下的。

事实上，ds 在后面的代码中并没有用到，所以也可以不赋初值。

然后接下来调用了 display string 的"函数"。这个函数内部的实现我们待会说，先回顾一下 call 和 ret。call 做的，是把下一条指令的 eip 压入栈中，然后 jmp 到 DispStr 表示的偏移处。ret 则是把栈顶赋给 eip。

然后是 jmp $。后面还有另一处用到了 $$。对于这两个标志，官方文档中的解释是：

NASM supports two special tokens in expressions, allowing calculations to involve the current assembly position: the $ and $$ tokens. $ evaluates to the assembly position at the beginning of the line containing the expression; so you can code an infinite loop using JMP $. $$ evaluates to the beginning of the current section; so you can tell how far into the section you are by using ($-$$).

此处可以简单理解为当前位置偏移量和所在节偏移量。我们这个程序中只有一个所谓的节，所以可以理解为程序开始的位置，也就是 07c00h。

jmp $ 的含义就是"跳转到当前指令"。这显然会是一个无限的循环。

最后三行都是我们学过的伪指令。db dw dd 是用来填放数据的，对应 byte, word, double word（字节，字，双字）。

$-$$ 可以理解为这条伪指令前面的部分已经占了多大。times 的意思是重复。显然的这个伪指令的意思就是填充 0 到 510 字节。

最后两个字节比较特殊，是 BIOS 识别引导扇区的依据，必须是 0xaa55。

如果不是 0xaa55 会发生什么？BIOS 会因为找不到启动引导盘而异常退出。你会在 bochs 收到一条这样的报错：[BIOS ] No bootable device.

接下来分析函数内的部分。

1
2
3
4
5
6
7
8
9
DispStr:
	mov	ax, BootMessage
	mov	bp, ax			; ES:BP = string address
	mov	cx, 16			; CX = string length
	mov	ax, 01301h		; AH = 13,  AL = 01h
	mov	bx, 000ch		; RED/BLACK
	mov	dl, 0
	int	10h
	ret

这个函数其实就是在调用中断处理程序。

前两行是在设置 bp 寄存器。事实上，变址寄存器并不是不能直接用立即数赋值，所以直接改成 mov bp, BootMessage 并没有什么问题。

es 前面设置过了。现在 es:bp 指向的是我们要显示的字符串的地址了。接下来的几行指令也是类似的，在设置调用的参数。然后 int 10h 调用中断处理程序。

我们大一上时学过这个。我们最熟悉的应该是 21h。大多数的中断例程都是通过 ah 来传递功能编号。我们这里调用的也许是 10h 号中断的 13h 号功能。

这个中断的相关信息我找到了这一篇 blog。可以参考一下，大概是差不多的意思。

xygg 太强了，什么都知道。官方文档在这里。

好像也没什么好解释的，就是调用了个 bios 里的中断处理程序显示了个字符串。

关于中断处理程序的组成，之前学过，但暂时还不需要，就不扯了。

1.5.3 反汇编

反汇编在这里是为了更好的理解代码的逻辑，观察代码实际编译的效果。

nasm 不仅提供了汇编的功能，也提供了反汇编的功能。你可以使用 ndisasm 进行反汇编。

具体的，我们使用下面的指令：

1
2
3
4
5
6
7
# 直接执行 ndisasm 可以看到它的帮助
# 课本里的 -o 0x7c00 是 origin 的意思，类似 org 0x7c00，是告诉反汇编程序这段代码是被装载在 0x7c00 处的
# 个人建议不加
ndisasm -o 0x7c00 boot.bin > disboot.asm
ndisasm -o boot.bin > disboot.asm
# 用 objdump 也可以
objdump -b binary -D -m i8086 -M intel boot.bin

为什么我不建议加 -o 0x7c00 呢。因为它会使 call 和 jmp 指令反汇编出来的东西“看上去不一样”。实际上这两在这里都是相对寻址，但是如果你不仔细对比机器码看的话，很容易产生误解。而且不加这条的话，mov ax, BootMessage 的反汇编效果会更加明显，更能体现出 org 指令的作用。

这里就不给出反汇编的代码了，只用看前几行就行，因为它会把你填充的数据和 "hello os" 也当成指令反汇编。

1.5.4 bochs 调试

关于 debugger 相关的文档在这里。

也可以参考书上这个图。

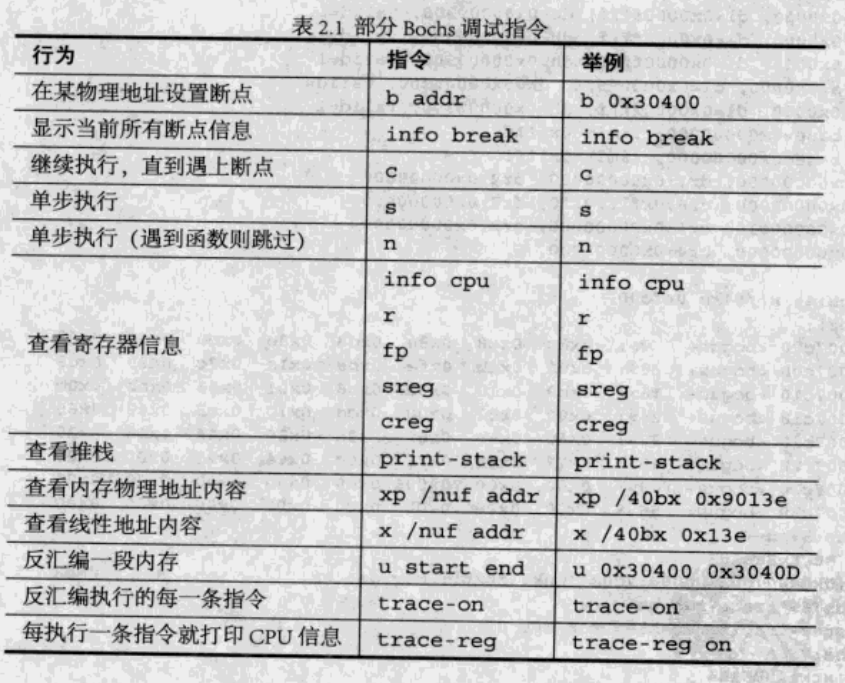
debug

查看 gdt ldt 可以直接 info gdt。

发表于
本文字数： 3.7k 阅读时长 ≈ 6 分钟

原题链接：https://codeforc.es/contest/1707/problem/C[https://codeforc.es/contest/1707/problem/C]

(家里网络不是很好，最近主站经常上不去，只好上镜像了)

题目大意

给你一个错误的求最小生成树的算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vis := an array of length n
s := a set of edges

function dfs(u):
    vis[u] := true
    iterate through each edge (u, v) in the order from smallest to largest edge weight
        if vis[v] = false
            add edge (u, v) into the set (s)
            dfs(v)

function findMST(u):
    reset all elements of (vis) to false
    reset the edge set (s) to empty
    dfs(u)
    return the edge set (s)

输入一个无重边无自环的联通无向图，且第 \(i\) 条边的边权为 \(i\)。问你调用 findMST(1), findMST(2), ..., findMST(n) 之后，哪些真的找到了 MST。

思路分析

比赛时毫无思路。第二次打 div1，这场的 A 太吓人了，想了老半天，中途一度想润，看到约好一起打的同学已经罚了一发了，只好硬着头皮打下去。结果最后还是掉分了呜呜呜，刚上的橙24小时不到又回去了呜呜呜。

扯歪了，回到这道题上来。

首先，这道题的边权设定，意味着边权两两不同，意味着 MST 有且只有一个。我们可以直接确定出这棵 MST 和不在 MST 里的是哪些边。

这个错误代码的特点是，它用了 DFS。DFS 意味着：访问到一个点后，回溯前，这个点所有的边都会被扫一遍。

因此，我们可以看出第一个问题：

如果边 \((u, v)\) 不在 MST 内，我们假设在 MST 中的边都能正常经过（或者说我们假设不合法边只有这一条）。

那在 DFS 经过 u 之后，必须在回到 u 之前先到达 v。换言之，MST 上必须存在一条不需要经过之前已经经过的点的路径，来从 u 到达 v。

也就是，从满足这个条件：把 v(或 u) 当作 MST 的根时，在 u(或 v) 子树内的点，的点开始 DFS，才可能满足这个要求。其它点必然在回溯到 u 或 v 时走到 (u, v) 这条边。

我们再观察一下 DFS 进行的方式：是从小到大遍历当前点的边。

那有没有可能说，尽管满足了上面的条件，也就是虽然存在一条 MST 上的路径能走到 v，但却选择了 (u, v) 的情形呢？

答案是不可能的，如果先选了 (u, v)，那意味着 MST 内的那条边是更大的。那我们把 MST 内的那条边换成 (u, v)，因为已经知道 u 到 v 有路径连着了，换成 (u, v) 后它依然是个生成树，而且边权和就更小了，这与我们已经确定的 MST 是矛盾的。

综上，我们可以说上面这个条件是一个充分且必要的条件。

换言之，你可以对于每条边求出能不经过这条边的 DFS 起点。最后扫一遍看看哪个点可以不经过任何不合法边就行了。

处理时，我们可以假定一个根，然后我们会看到两种情形：

前者，子树互相包含的情况。下面那个点直接取子树，上面的点就是除了子树内包含下面那个点的儿子的那棵子树外，其它的点都可以取。

后者，就是直接取二者的子树了。

用 dfs 序啊树状数组之类的东西搞一下就行了。我用的是链剖。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int N = 1e5 + 5, M = 2e5 + 5;
int n, m, f[N], ex[M][2], ce; // 注意 ex 的大小！
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
int head[N], nex[N << 1], to[N << 1];
inline void addEdge(int u, int v) {
    static int cc = 0;
    nex[++cc] = head[u], head[u] = cc, to[cc] = v;
}
int dfn[N], cnt[N], hson[N], dad[N], topf[N], A[N];
void dfs1(int u, int fa) {
    cnt[u] = 1, dad[u] = fa;
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == fa) continue;
        dfs1(to[i], u);
        cnt[u] += cnt[to[i]];
        if(cnt[to[i]] > cnt[hson[u]]) hson[u] = to[i];
    }
}
void dfs2(int u, int top) {
    static int dn = 0;
    dfn[u] = ++dn, topf[u] = top, A[dn] = u;
    if(hson[u]) dfs2(hson[u], top);
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == dad[u] || to[i] == hson[u]) continue;
        dfs2(to[i], to[i]);
    }
}
int mark[N];
inline int lowbit(int x) {
    return x & -x;
}
inline void add(int x, int d) {
    while(x <= n) mark[x] += d, x += lowbit(x);
}
inline int sum(int x) {
    int ans = 0;
    while(x) ans += mark[x], x -= lowbit(x);
    return ans;
}
int main() {
    //freopen("in.txt", "r", stdin);
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) f[i] = i;
    for(int i = 1; i <= m; i++) {
        int u, v, a, b; 
        scanf("%d%d", &u, &v);
        a = find(u), b = find(v);
        if(a != b) {
            addEdge(u, v), addEdge(v, u);
            f[a] = b;
        } else {
            ex[++ce][0] = u, ex[ce][1] = v;
        }
    }
    dfs1(1, 0);
    dfs2(1, 1);
    for(int i = 1; i <= ce; i++) {
        int u = ex[i][0], v = ex[i][1];
        if(dfn[v] + cnt[v] > dfn[u] && dfn[u] > dfn[v]) swap(u, v);
        if(dfn[u] + cnt[u] > dfn[v] && dfn[v] > dfn[u]) {
            add(dfn[v], 1), add(dfn[v] + cnt[v], -1); add(1, 1);
            while(dad[v] != u) {
                if(topf[v] == topf[u]) v = A[dfn[u] + 1];
                else if(dad[topf[v]] == u) v = topf[v];
                else v = dad[topf[v]];
            }
            add(dfn[v], -1), add(dfn[v] + cnt[v], 1);
        } else {
            add(dfn[v], 1), add(dfn[v] + cnt[v], -1);
            add(dfn[u], 1), add(dfn[u] + cnt[u], -1);
        }
    }
    /*for(int i = 1; i <= n; i++) {
        printf("%d %d %d %d %d %d\n", dfn[i], sum(dfn[i]), A[dfn[i]], cnt[i], topf[i], dad[i]);
    }*/
    for(int i = 1; i <= n; i++) {
        if(sum(dfn[i]) == m - n + 1) printf("1");
        else printf("0");
    }
    puts("");
    return 0;
}

发表于 分类于
本文字数： 5.5k 阅读时长 ≈ 9 分钟

原题链接：https://codeforces.com/contest/1701/problem/E

题目大意

问你当前序列有多少个三元组满足 且 。 是一个最开始给定的值。每次操作要求你往序列里（如果不存在）加入 或是（如果存在）删去 ，然后输出满足要求的三元组的数量。（数都在 内）

思路分析

方法一

这个是我看到题之后想到的。

加入一个点时，把这个点的贡献加入答案；删去时，把这个点的贡献从答案中删除。

一个点 产生的贡献有三种情况：

  1. 这个点是三元组里的 。记与这个点距离小于等于 ，且在它的后面的点有 个，这种情况的贡献就是 。
  2. 作为三元组里的 。同理，记与这个点距离小于等于 ，且在它的前的点有 个，这种情况的贡献就是 。
  3. 作为三元组的中间点 。它的贡献就是分别处在左右两侧且距离不超过 d 的点对数量。

前两种情形很好处理。用树状数组维护一下点的数量前缀和 就行了。

情况三，我们用 表示 到 有多少个点（数量前缀和），用 表示这个点是否存在。它的贡献是：

所以我们用树状数组维护 ，线段树维护区间 之和和 之和（有效点的数量）。

标记的传递、点的有效和无效化、维护的顺序可以参考代码。有亿点小细节，我调了蛮久。

方法二

这个做法来自官方题解。个人觉得它更加简洁好写。

我们记每个 往后距离不超过 的点的数量为 ，用 表示 上是否有点。显然的，我们的答案是：

用线段树维护有效的 和 就行了。

平方和维护的方法有很多种，什么 3*3 的矩阵啊，或是直接按着 之类的，这里不再赘述，具体参考代码。

代码

方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
// 产生一个点的变化时，我们要考虑三个东西：
// 1. 这个点是三元组的起点
// 2. 这个点是三元组的终点
// 3. 这个点是三元组的中点
// 前两者非常好处理，存一下点的数量就行了
// 第三个就是求 \sum (s[i + d] - s[x]) * vis[i]
// 线段树维护一下就行
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5; //8 + 5;
int q, d, cnt[N];
inline int lowbit(int x) {
    return x & -x;
}
inline void add(int x, int v) {
    while(x <= N - 5) {
        cnt[x] += v;
        x += lowbit(x);
    }
}
inline int sum(int x) {
    int ans = 0;
    while(x) ans += cnt[x], x -= lowbit(x);
    return ans;
}
#define ls (u << 1)
#define rs ((u << 1) | 1)
ll tr[N << 2], tag[N << 2], siz[N << 2];
inline void maintain(int u) {
    tr[u] = tr[ls] + tr[rs];
    siz[u] = siz[ls] + siz[rs];
}
inline void upd(int u, ll d) {
    tr[u] += d * siz[u];
    tag[u] += d;
}
inline void pushdown(int u) {
    if(tag[u]) {
        upd(ls, tag[u]), upd(rs, tag[u]);
        tag[u] = 0;
    }
}
void update(int u, int l, int r, int ql, int qr, ll d) {
    if(r < ql || l > qr) return;
    if(ql <= l && r <= qr) return upd(u, d);
    int mid = (l + r) >> 1;
    pushdown(u);
    update(ls, l, mid, ql, qr, d), update(rs, mid + 1, r, ql, qr, d);
    maintain(u);
}
void edit(int u, int l, int r, int x) {
    if(r < x || l > x) return;
    if(l == r) {
        siz[u] ^= 1;
        tr[u] = siz[u] * sum(min(x + d, N - 5));
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(u);
    edit(ls, l, mid, x), edit(rs, mid + 1, r, x);
    maintain(u);
}
ll query(int u, int l, int r, int ql, int qr) {
    if(r < ql || l > qr) return 0;
    if(ql <= l && r <= qr) return tr[u];
    int mid = (l + r) >> 1;
    pushdown(u);
    return query(ls, l, mid, ql, qr) + query(rs, mid + 1, r, ql, qr);
}
void debug(int u, int l, int r) {
    if(l == r) {
        printf("i=%d s[i+d]=%lld siz[i]=%lld\n", l, tr[u], siz[u]);
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(u);
    debug(ls, l, mid), debug(rs, mid + 1, r);
}
int vis[N];
int main() {
    memset(vis, -1, sizeof(vis));
    scanf("%d%d", &q, &d);
    ll res = 0;
    for(int i = 1; i <= q; i++) {
        int x; scanf("%d", &x);
        vis[x] *= -1;
        // add(x, vis[x]); 不能在这里更新树状数组
        // 作为起点
        ll t = sum(min(x + d, N - 5)) - sum(x), t2;
        res += vis[x] * t * (t - 1) / 2;
        // 作为终点
        t = sum(x - 1) - sum(max(0, x - d - 1)); //你要求的是 [x-d, x-1]！
        res += vis[x] * t * (t - 1) / 2;
        // 作为中点
        t = query(1, 1, N - 5, max(1, x - d + 1), x - 1);
        // t2使用的是树状数组里的数据 t1使用的是线段树里的数据 我们需要保证这两者是同步的
        // 因此 要么一起放到前面更新 要么一起放到后面更新
        t2 = (ll)(sum(x - 1) - sum(max(x - d, 0))) * sum(x); // 这里要记得开ll！
        res += vis[x] * (t - t2);
        // 输出答案
        printf("%lld\n", res);
        // 更新 S[i+d] 的维护
        add(x, vis[x]);
        update(1, 1, N - 5, max(x - d, 1), N - 5, vis[x]);
        edit(1, 1, N - 5, x); // 注意这个必须在后面 不然会被额外upd一次
        /*if(i >= 5) {
            debug(1, 1, N - 5);
            for(int j = 1; j <= N - 5; j++) printf("%d(%d) ", j, sum(j) - sum(j - 1));
            puts("");
        }*/
    }
    return 0;
}

方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
// ai^2 + 2xai + x^2
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
ll tr[2][N << 2], tag[N << 2], siz[N << 2];
int m, cnt[N];
inline int lowbit(int x) {
    return x & -x;
}
inline void add(int x, int d) {
    while(x <= N - 5) {
        cnt[x] += d;
        x += lowbit(x);
    }
}
inline int sum(int x) {
    int an = 0;
    while(x) an += cnt[x], x -= lowbit(x);
    return an;
}
#define ls (u << 1)
#define rs ((u << 1) | 1)
inline void maintain(int u) {
    tr[0][u] = tr[0][ls] + tr[0][rs];
    tr[1][u] = tr[1][ls] + tr[1][rs];
    siz[u] = siz[ls] + siz[rs];
}
inline void add(int u, ll d) {
    tr[1][u] += 2ll * d * tr[0][u] + d * d * siz[u];
    tr[0][u] += d * siz[u];
    tag[u] += d;
}
inline void pushdown(int u) {
    if(tag[u]) {
        add(ls, tag[u]), add(rs, tag[u]);
        tag[u] = 0;
    }
}
void update(int u, int l, int r, int ql, int qr, ll d) {
    if(r < ql || l > qr) return;
    if(ql <= l && r <= qr) return add(u, d);
    int mid = (l + r) >> 1;
    pushdown(u);
    update(ls, l, mid, ql, qr, d), update(rs, mid + 1, r, ql, qr, d);
    maintain(u);
}
void edit(int u, int l, int r, int x, ll d) {
    if(r < x || l > x) return;
    if(l == r) {
        siz[u] += d;
        ll fi = sum(min(N - 5, x + m)) - sum(x);
        tr[0][u] += d * fi;
        tr[1][u] += d * fi * fi;
        return; 
    }
    int mid = (l + r) >> 1;
    pushdown(u);
    edit(ls, l, mid, x, d), edit(rs, mid + 1, r, x, d);
    maintain(u);
}
ll getAns() {
    return (tr[1][1] - tr[0][1]) / 2;
}
int vis[N];
int main() {
    memset(vis, -1, sizeof(vis));
    int q, d;
    scanf("%d%d", &q, &d);
    m = d;
    for(int i = 1; i <= q; i++) {
        int x; scanf("%d", &x);
        vis[x] *= -1;
        add(x, vis[x]);
        edit(1, 1, N - 5, x, vis[x]);
        update(1, 1, N - 5, max(1, x - d), x - 1, vis[x]);
        printf("%lld\n", getAns());
    }
    return 0;
}

发表于 分类于
本文字数： 3.9k 阅读时长 ≈ 7 分钟

原题链接：https://codeforces.com/contest/1701/problem/E

题目大意

给你一个字符串 s，要你通过下面的操作变成字符串 t，同时要求操作数最小。（光标初始在 s 的最后一个字符的右边）

  1. home 光标移动到第一个字符左边
  2. left 和 right 光标移动一个单位距离
  3. backspace 删除光标前的那个字符
  4. end 光标移动到最后一个字符右边

思路分析

比赛时统计答案的部分没调出来。

一眼 dp。有一个很明显的结论：在确定了你要留下的东西之后，你先把右边该删的删完再去删左边要删的，显然是更优的。所以我们可以分开 dp，然后把从左往右的答案和从右往左的答案拼起来。

用 表示光标在i的右边，且从右往左匹配到第j个字母的最小操作数， 表示光标在i的左边，且从左往右匹配到第j个字母的最小操作数。于是有下面的方程：

从左到右扫求出 g，从右往左扫求出 f。直接枚举 k 的话是 。加一个数组来存下对于每个 j， 和 的最小值，就可以优化到 。

然后统计答案。

统计答案的细节如下：

最直观的，我们需要取 。

对于从右往左一路删到底的情况，我们在从右往左匹配到第一个字符后，还要考虑它前面是不是还有多余的字符要删，如果有，那我们需要 left 一次，然后删掉多余的字符。

即：。

然后，还有一种较为麻烦的情形：我们在 dp 时是默认光标跟着匹配过程移动的，可有的时候，中间那个连续段，我们并不需要把光标移进去，因为那段中间没有任何需要删的内容。我们删到那一段右边后就可以直接润去删它的左边了。

即：，当 时。

以及在这种情形下也有一个特判： 且 ，并不需要 里的那次 home。

即：

我们统计答案用的必须是有效的 和 ，也就是说这两个数不可以是 。

对于前面几种情形，直接 的枚举就可以统计。

对于中间有一段不需要把光标移进去的情形，我们可以想到一个很直观的三重循环：枚举 i, j 和 k。这样会 tle on test 20。所以我们需要加一点优化。

一个很明显的贪心结论：既然你中间要弄出一段来，那这一段一定是能弄多长就弄多长吧。

以及另一个明显的结论：如果 ，根据我们的转移方程， 显然不可能不是 ，不然它可以往左边的 i+k 转移使得前者不是 。

由于我们是从左往右枚举 i 的。那如果从 i, j 这里凑出了一段来，那后面枚举到 i+1, j+1 的时候再去枚举 k 就没有必要了，因为不可能会比前面更优。

所以我们直接把扫过的用上的 设成 。及时中断不需要的循环。

代码

不要吐槽为什么 rep 和 for 混着用。因为是比赛时敲的，顺手就敲进去了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int N = 5e3 + 5, INF = 0x3f3f3f3f;
int n, m; char s[N], t[N]; int f[N][N], mi[N], g[N][N];
int main() {
    //freopen("in.txt", "r", stdin);
    int T; scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) g[i][j] = f[i][j] = INF;
        scanf(" %s %s", s + 1, t + 1);
        rep(i, 1, m) mi[i] = INF;
        for(int i = n; i >= 1; i--) {
            for(int j = m; j >= 1; j--) {
                if(s[i] != t[j]) continue;
                if(j == m) {
                    f[i][j] = n - i;
                    continue;
                }
                /*for(int k = i + 1; k <= n; k++) {
                    if(s[k] == t[j + 1]) f[i][j] = min(f[i][j], f[k][j + 1] + k - i);
                }*/
                if(mi[j + 1] != INF) f[i][j] = min(f[i][j], mi[j + 1] - i);
                else break;
            }
            for(int j = 1; j <= m; j++) mi[j] = min(mi[j], f[i][j] + i);
        }
        rep(i, 1, m) mi[i] = INF;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(s[i] != t[j]) continue;
                if(j == 1) {
                    g[i][j] = 1 + (i - 1) * 2;
                    continue;
                }
                /*for(int k = 1; k <= i - 1; k++) {
                    if(s[k] == t[j - 1]) g[i][j] = min(g[i][j], g[k][j - 1] + i - k + i - k - 1);
                }*/
                if(mi[j - 1] != INF) g[i][j] = min(g[i][j], mi[j - 1] + 2 * i);
                else break;
            }
            rep(j, 1, m) {
                if(g[i][j] == INF) continue;
                mi[j] = min(mi[j], g[i][j] - 2 * i - 1);
            }
        }
        int res = INF;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(s[i] != t[j]) continue;
                //printf("i=%d j=%d f=%d g=%d\n", i, j, f[i][j], g[i][j]);
                res = min(res, g[i][j] + f[i][j]);
                if(j == 1 && g[i][j] != INF) {
                    int d = i == 1 ? 0 : 1;
                    res = min(res, f[i][j] + d + i - 1); // 顺着删到后面去
                }
                /*if(j == m && f[i][j] != INF) {
                    res = min(res, g[i][j] + n - i); // 其实会被算过，不需要这个也行
                }*/
            }
        }
        //printf("ss%d\n", res);
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(s[i] != t[j]) continue;
                for(int k = j + 1; k <= m; k++) {
                    if(s[i + k - j] != t[k]) break;
                    if(g[i][j] == INF || f[i + k - j][k] == INF) break;
                    //printf("i=%d %d j=%d %d: g=%d f=%d\n", i, i + k - j, j, k, g[i][j], f[i + k - 1][k]);
                    if(j == 1) {
                        int d = i == 1 ? 0 : 1;
                        res = min(res, f[i + k - j][k] + d + (i - 1) * 2);
                    }
                    /*if(k == m) {
                        res = min(res, g[i][j] + n - (i + k - j));
                    }*/
                    res = min(res, g[i][j] + f[i + k - j][k]);
                    f[i + k - j][k] = INF;
                }
            }
        }
        if(res == INF) printf("-1\n");
        else printf("%d\n", res);
    }
    return 0;
}

发表于 更新于 分类于
本文字数： 2.1k 阅读时长 ≈ 3 分钟

原题链接：https://codeforces.com/contest/1700/problem/E

题目大意

给你一个排列 A 和排列 B，你要通过下面的操作把 A 弄成 B。你有一个“力量”值 ，对于每个 ，选择一个 ，交换 和 的位置。例如 1 3 2 交换 1 和 2，结果是 2 3 1。问你 A 能变成的不同 B 有多少种（给出了 B 的部分位置的值，其它位置的值可以随便取，只要是个排列就行）。

思路分析

这题太抽象了。比赛时连怎么换的都绕不清楚，一直满脑子的什么连有向边什么环什么链什么玩意，更别提计数了。

首先，因为从头到尾换的都是值，所以我们可以把其中一个排列“标准化”。让我们来想一想，如果手头有确定的排列 A 和排列 B，我要怎么把 A 换到 B 呢？

例如：A: 5 4 2 3 1, B: 3 1 4 2 5

将 B 标准化后：A: 4 3 5 2 1, B: 1 2 3 4 5

此时我们从左往右看，首先要把 1 弄到正确的位置上，于是我们交换且只能交换 1 和 4（因为每个值只能进行一个操作，且这个操作的对象必须是比它大的数，如果你现在不换 1，后面 1 就不会再被换到了）。此时变成了：A: 1 3 5 2 4, B: 1 2 3 4 5

换完 1 之后，1 显然是不会再被动的（因为只能往大的方向换），所以我们无视 1。这个时候 2 又变成了最小，我们再去用同样的道理去换 2。直到所有数字都到达正确的位置上。

通过上面的例子，我们不难看出，对于确定的 A 和 B，我们有且只有一个固定的替换方式，来使得 A 变成 B。

而我们要问的是 B 的种数，那我们就需要确认，这个替换过程中，是否一直都满足 。

这里有一个结论：必须有 。

结合上面的标准化后的例子很容易理解：首先 是肯定要的。而我们的替换过程一直是在让 和此时的 替换，因此 是必要的。

而如果 ，那这个 肯定会被前面某个 的 替换。而由于 k 在 i 前面，所以显然有 ，这个点不考虑也罢。因此， 的要求是充分且必要的。

接下来考虑计数的问题。有了这个结论之后，问题就变得简单了不少。我们的问题转化为求满足 的排列数量。

我们把没有确定对应的 弄出来排个序，然后我们从小到大枚举缺的 ，这样就保证了后面枚举到的 的可选位置范围比前一个大。每个 的可选位置数乘起来就是我们要的答案了。

具体看代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int N = 2e5 + 5;
int n, A[N], B[N], s, C[N], cc, D[N], cd; bool vis[N];
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &s);
        for(int i = 1; i <= n; i++) scanf("%d", A + i), vis[i] = 0;
        cc = cd = 0;
        for(int i = 1; i <= n; i++) {
            scanf("%d", B + i);
            if(B[i] == -1) C[++cc] = A[i];
            else vis[B[i]] = 1;
        }
        bool fail = 0;
        for(int i = 1; i <= n && !fail; i++) {
            if(B[i] != -1) {
                if(A[i] - B[i] > s) fail = 1;
                continue;
            }
        }
        if(fail) {
            puts("0"); 
            continue;
        }
        sort(C + 1, C + cc + 1);
        for(int i = 1; i <= n; i++) {
            if(!vis[i]) D[++cd] = i;
        }
        int p = 0; ll ans = 1;
        for(int i = 1; i <= cd; i++) {
            while(p < cc && D[i] >= C[p + 1] - s) p++;
            if(p - i + 1 <= 0) {
                ans = 0;
                break;
            }
            ans = ans * (ll)(p - i + 1) % mod;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

发表于 更新于 分类于
本文字数： 3k 阅读时长 ≈ 5 分钟

原题链接：https://codeforces.com/contest/1700/problem/F

题目大意

给你两个 2*n 的矩阵。上面只有 0 和 1。你每次操作能交换两个相邻位置上的数字。问你最少需要多少次操作才能把矩阵 1 转换成矩阵 2。

思路分析

一道需要仔细观察和猜结论的贪心题。

首先，如果两个矩阵 1 的数量不一样，无解。

然后，这个所谓的交换，可以直接看成 1 的移动。我们假设 1 的数量为 m。

然后你会发现，问题转化成了这样：有 m 个目标点和 m 个起点构成的二分图，边权是曼哈顿距离，要你求一个权值和最小的完美匹配。

这有什么意义嘛。没有。所以我比赛没写出来。

我们再思考一下：单论列的分配，我们可以发现，前 i 个目标，分配给前 i 个起点，肯定不会亏。也就是说，只有一行时，起点和目标点应该是按从左到右的顺序一一对应的。

此外，有一个非常重要且明显的结论：一个点如果要变行，最多只会变一次。

这里就产生了一种非常暴力的做法：枚举每个点是否要变行，先变完行再按上面的贪心策略求解。

我们再进一步观察一下，变行后，答案会发生什么变化。

假如你用一种变行方式求出来的解是 ，那么你换另一种变行方案，它肯定要一个上去一个下来（因为行的数量要对应）。

我们用 表示初始矩阵第一行的 m 个点，用 表示第二行的 n 个点。

同理用 和 表示目标矩阵的。并且记上下移动的次数为 。

此时有：

题解的贪心策略我压根就没看懂。所以我们来看看能不能 dp 吧。

我们可以用 f[i] 表示上面已经匹配了 i 个点，此时的最小步数。我们是从左往右扫的，这个玩意显然是没有后效性的。而且假如我们当前已经扫了 k 个点，那下面就匹配了 k - i 的点。可以得到一个转移方程（当前点为 ）：

或者说

但是这样是 的啊，直接 dp 是自然不行的。

算了，还是看看题解的做法是什么吧。

题解把 的答案做了更进一步的转换：我们记 表示初始矩阵第 i 行前 j 个位置共有多少个 1， 表示目标矩阵的对应值。

于是，我们有 。

用心去感受一下，这个式子是对的。

重要的是，这个式子把难以处理的点坐标差值变化转化成了很好处理的前缀和的区间变化。

例如，如果 的点被挪到了 ，那它会使得 全部减少 1，而 全部加 1。

我们记 ，则有

当 的点被挪到了 ，它会使得 全部减少 1，而 全部加 1。

我们这个式子里面的 都是以绝对值出现的，而由移动引起的变化方向是相反的。并且，从定义上不难看出，随着 i 的移动， 值一次的变化不会超过 1。

所以，我们可以这样贪心：每当我们扫到一个位置，它的 和 异号时，我们进行交换（因为每次变化都最多是 1，所以此处一定有点可换），把点从正的那一行换到负的那一行（首先 s 加一，然后 i 后面的 delta 都要变）。

因为你的 s 只会加 1，而这两个数的绝对值分别少了 1，是赚的。这样至少在当前位置上看，它是赚的。

至于为什么这个策略在全局是对的，题解的证明太长了。我感性地理解一下：

首先你这两 delta 到最后肯定都是 0，因为数量会对上。

另外，这样换的话，你的 delta 绝对值是在减少的。我们知道 delta 每次变化最多是 1。

如果你这里减少了绝对值，那下一次变化也是不会亏的（减到 0，后面变成 1，如果你不减的话原本也是 1，这个 1 还可能多影响了几步，不亏；没减到 0，后面要么加回来要么变得更少，不可能比不减的代价多，不亏）。

总之不懂啊，好难。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
int n, A[2][N], B[2][N], d[2][N];
inline int sgn(int x) {
    if(x == 0) return 0;
    return x > 0 ? 1 : -1;
}
int main() {
    scanf("%d", &n);
    int cn = 0;
    for(int i = 0; i < 2; i++) for(int j = 1; j <= n; j++) {
        scanf("%d", A[i] + j), cn += A[i][j];
        A[i][j] += A[i][j - 1];
    }
    for(int i = 0; i < 2; i++) for(int j = 1; j <= n; j++) {
        scanf("%d", B[i] + j), cn -= B[i][j];
        B[i][j] += B[i][j - 1];
    }
    if(cn != 0) {
        puts("-1");
        return 0;
    }
    int up = 0, down = 0; ll res = 0;
    for(int i = 1; i <= n; i++) {
        d[0][i] = A[0][i] - B[0][i] + up;
        d[1][i] = A[1][i] - B[1][i] + down;
        if(sgn(d[0][i]) * sgn(d[1][i]) == -1) {
            if(d[0][i] > 0) up--, down++, d[0][i]--, d[1][i]++;
            else up++, down--, d[0][i]++, d[1][i]--;
            res++;
        }
        res += abs(d[0][i]) + abs(d[1][i]);
    }
    printf("%lld\n", res);
    return 0;
}

发表于 分类于
本文字数： 3.1k 阅读时长 ≈ 5 分钟

原题链接：https://codeforces.com/contest/1700/problem/E

题目大意

给你一个 n*m 的矩阵，矩阵上的元素是 nm 的排列。要求：能够找到一条路径遍历所有的点（每个点可经过多次），记每个点在第 xi 步第一次被访问，要求有 x1 < x2 < x3 ...。现在问你：原本的矩阵是否满足要求？如果不满足，能否通过1次交换使得它满足要求，可能的交换种类有多少种？

思路分析

一道简单的暴力题。比赛时没想清楚。

一个很明显的结论：1 肯定是起点，对于每个大于 1 的点，它的周围至少要有一个小于它的点。如果所有的点都可以满足这个要求，那么矩阵满足要求。

再考虑交换会发生什么：它只会改变交换的点自身和它周围的点的这个状态。

这意味着：我们的交换至少要包含一个不满足要求的点（或是那个点周围的点），每次交换最多只会影响 10 个点（两个被交换点和它的相邻点）的状态。

所以，我们找到一个不满足要求的点之后，直接枚举它和它周围的这 5 个点作为其中一个交换点，然后枚举所有点作为另外一个交换点，动态地维护、计算图上有多少个点满足要求就行了。复杂度大概是 的。

去重什么的就自己看着办就行了。我是存起来排序 unique 的。直接记录然后减也是可以的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 4e5 + 5;
const int zl[5][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}, {0, 0}};
int n, m, A[N], f[N], tot, cc;
inline int id(int x, int y) {
    return x * m + y;
}
inline int isBad(int x, int y) {
    if(A[id(x, y)] == 1) return 0;
    int v = A[id(x, y)];
    if(x > 0 && A[id(x - 1, y)] < v) return 0;
    if(y > 0 && A[id(x, y - 1)] < v) return 0;
    if(x < n - 1 && A[id(x + 1, y)] < v) return 0;
    if(y < m - 1 && A[id(x, y + 1)] < v) return 0;
    return 1;
}
inline bool inSqu(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < m;
}
bool vis[N];
inline bool judge(int x, int y, int p, int q) {
    int i1 = id(x, y), i2 = id(p, q), del = 0;
    int tx, ty, d, i3;
    swap(A[i1], A[i2]);
    for(int i = 0; i < 5; i++) {
        // for i1
        tx = x + zl[i][0], ty = y + zl[i][1];
        if(inSqu(tx, ty)) {
            i3 = id(tx, ty);
            if(!vis[i3]) {
                vis[i3] = 1, d = isBad(tx, ty);
                if(d ^ f[i3]) {
                    if(d > 0) del--;
                    else del++;
                }
            }
        }
        // for i2
        tx = p + zl[i][0], ty = q + zl[i][1];
        if(!inSqu(tx, ty)) continue;
        i3 = id(tx, ty);
        if(!vis[i3]) {
            vis[i3] = 1, d = isBad(tx, ty);
            if(d ^ f[i3]) {
                if(d > 0) del--;
                else del++;
            }
        }
    }
    // clear
    for(int i = 0; i < 5; i++) {
        // for i1
        int tx = x + zl[i][0], ty = y + zl[i][1];
        if(inSqu(tx, ty)) vis[id(tx, ty)] = 0;
        // for i2
        tx = p + zl[i][0], ty = q + zl[i][1];
        if(!inSqu(tx, ty)) continue; // 注意上面不能 continue 哦，因为下面的还要算的
        vis[id(tx, ty)] = 0;
    }
    swap(A[i1], A[i2]);
    return del == tot;
}
struct Op {
    int a, b;
    Op(int s = 0, int t = 0): a(s), b(t) {
        if(a > b) swap(a, b);
    }
    bool operator < (const Op &B) const {
        if(a != B.a) return a < B.a;
        return b < B.b;
    }
    bool operator == (const Op &B) const {
        return a == B.a && b == B.b;
    }
}L[N * 5];
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n * m; i++) scanf("%d", A + i);
    int bx = -1, by = -1;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < m; j++) {
            if(isBad(i, j)) {
                tot += (f[i * m + j] = 1);
                bx = i, by = j;
            }
        }
    }
    if(bx == -1) return puts("0"), 0;
    for(int i = 0; i < 5; i++) {
        int x = bx + zl[i][0], y = by + zl[i][1];
        if(x < 0 || x >= n || y < 0 || y >= m) continue;
        for(int p = 0; p < n; p++) {
            for(int q = 0; q < m; q++) {
                if(judge(x, y, p, q)) {
                    // printf("(%d, %d) - (%d, %d)\n", x, y, p, q);
                    L[++cc] = Op(id(x, y), id(p, q));
                }
            }
        }
    }
    if(cc == 0) return puts("2"), 0;
    sort(L + 1, L + cc + 1);
    cc = unique(L + 1, L + cc + 1) - L - 1;
    printf("1 %d\n", cc);
    return 0;
}

发表于 分类于
本文字数： 2.8k 阅读时长 ≈ 5 分钟

原题链接：https://codeforces.com/contest/1695/problem/D2

题目大意

给你一棵树。要求你指定一组基准点（询问） ，对于树上的每一个点 u，u 对基准点的最短距离形成的 k 元组 两两不同。问基准点（询问）至少要有多少个。

思路分析

这题比赛的时候没想清楚。

首先，一个很明显的结论，如果一个点有 n 个直接儿子，那么至少需要有 n - 1 个询问才能区分它的所有直接儿子。如果只有这个点本身，则不需要添加询问来区分。

于是，我们这样考虑：对于节点 u，我们试图去求区分以 u 的子树内的点需要多少个询问（我们默认 u 会有更上层的点来区分好，因此不去考虑根节点 u，只考虑它的直接和间接子节点）。我们将这个值记为 f[u]。

首先，我们需要区分儿子的子树，因此 f[u] += sum(f[v])。此外，对于 f[v] > 0 的点，意味着这个子节点可以被 u 上面的那个查询和 v 子树内本身已经有的查询来区分。因此，我们记录下 f[v] = 0 的儿子数量 c，我们需要给其中的 c - 1 个儿子进行询问。

故有转移方程：

dp 后得到的 f[u]，是在默认根节点 u 已经由非子树内节点区分的情况下，区分子树内点所需要的最小询问数。或者说默认 u 或 u 的某个父亲上有一个询问（这个询问不记在 f[u] 中，只是假设它存在）的情况下，区分子树内节点的最小询问数。

也因此，我们最终求出的这个 f[rt] 还需要加上 1 （也就是根节点上的询问）才是答案。枚举所有的根节点算一遍，取个 min，就是我们要的解。

然后 D1 与 D2 的区别就是换不换根而已了。

换根其实就是在换到 v 前，把当前这个根 u 的值重新算一遍（去掉 v 的影响，因为 v 已经不是 u 的儿子了），然后换到 v 时把 v 的值按着 dp 方程重新算一遍就行。典。具体参考代码。

代码

D1 O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
int head[N], nex[N << 1], to[N << 1], n, cc;
inline void addEdge(int u, int v) {
    nex[++cc] = head[u], head[u] = cc, to[cc] = v;
}
int f[N];
void dfs(int u, int fa) {
    int c = 0;
    f[u] = 0;
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == fa) continue;
        dfs(to[i], u);
        f[u] += f[to[i]];
        if(!f[to[i]]) c++;
    }
    if(c) f[u] += c - 1;
}
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        scanf("%d", &n); cc = 0;
        for(int i = 1; i <= n; i++) head[i] = 0;
        for(int i = 1; i < n; i++) {
            int u, v; scanf("%d%d", &u, &v);
            addEdge(u, v), addEdge(v, u);
        }
        int res = n - 1;
        for(int i = 1; i <= n; i++) {
            dfs(i, 0);
            res = min(res, f[i] + 1);
        }
        printf("%d\n", res);
    }
    return 0;
}

D2 O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e5 + 5;
int head[N], nex[N << 1], to[N << 1], n, cc;
inline void addEdge(int u, int v) {
    nex[++cc] = head[u], head[u] = cc, to[cc] = v;
}
int f[N], res, hav[N];
void dfs1(int u, int fa) {
    int c = 0;
    f[u] = hav[u] = 0;
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == fa) continue;
        dfs1(to[i], u);
        f[u] += f[to[i]];
        if(!f[to[i]]) c++;
    }
    if(c) {
        f[u] += c - 1;
        if(c > 1) hav[u] = 1;
    }
}
void dfs2(int u, int fa) {
    if(fa) {
        int c = 0; f[u] = 0;
        for(int i = head[u]; i; i = nex[i]) {
            f[u] += f[to[i]];
            if(!f[to[i]]) c++;
        }
        if(c) f[u] += c - 1;
        if(c > 1) hav[u] = 1; // 记住这个 hav 也是会变的
    }
    int fu = f[u];
    res = min(res, f[u] + 1);
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == fa) continue;
        if(f[to[i]]) f[u] = fu - f[to[i]];
        else f[u] = fu - hav[u];
        dfs2(to[i], u);
    }
}
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        for(int i = 1; i <= n; i++) head[i] = 0;
        scanf("%d", &n); cc = 0;
        for(int i = 1; i < n; i++) {
            int u, v; scanf("%d%d", &u, &v);
            addEdge(u, v), addEdge(v, u);
        }
        res = n - 1;
        dfs1(1, 0);
        dfs2(1, 0);
        printf("%d\n", res);
    }
    return 0;
}

发表于 分类于
本文字数： 2.7k 阅读时长 ≈ 5 分钟

原题链接：https://codeforces.com/contest/1695/problem/C

题目大意

给你一个 n * m 的矩阵 (n, m < 1001)。每个元素都是 1 或 -1。你每次只能往下或往右，问你能否找到一条路径使得路上的权值和为 0。

思路分析

比赛的时候只想到了 的做法。

首先，很显然的，步数是 n + m - 1。如果这是个奇数，无解。

然后，转换模型，权值和为 0，其实就是要有一半踩到 1。所以，用一个 n 位的二进制数 f[i][j] 表示从 (1, 1) 走到 (i, j)，手上的 1 可能是多少个。于是可以得到这样的 dp 方程：

1
2
if(A[i][j] == 1) f[i][j] = (f[i - 1][j] << 1) | (f[i][j - 1] << 1);
else f[i][j] = f[i - 1][j] | f[i][j - 1];

套上 bitset，可以通过此题。

但这个不是正解。我们仔细想一想，如果 (i, j) 处最多有 b 个 1，最少有 a 个 1。那么是不是意味着 [a, b] 以内的所有值都能在 (i, j) 找到呢？

我们可以感性的这样想：对于任意一条从左上角到右下角的路径，我们一定能找到另一条路径，使得这两条路径只有一个格子不一样。换句话说，通过挪动路径上的某个格子，你可以得到另外一条路径；任意两条路径间一定可以通过若干次的单格子变化得到。

而我们知道，每次只变化一个格子，那就意味着这条路径上 1 的变化量要么是 0 要么是 1。

因此，如果存在 a 个 1 的路径和 b 个 1 的路径，那么我们一定能够凑出 a 到 b 间的所有数目。

代码

bitset

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <cstdio>
#include <algorithm>
#include <bitset>
#include <iostream>
using namespace std;
const int N = 1e3 + 5;
int n, m, A[N][N];
bitset<N> f[N][N];
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) {
            scanf("%d", A[i] + j);
            if(A[i][j] == -1) A[i][j] = 0;
            f[i][j].reset();
        }
        if((n + m - 1) & 1) {
            puts("No");
            continue;
        }
        int aim = (n + m - 1) / 2;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(i == 1 && j == 1) {
                    if(A[1][1]) f[i][j].set(1, 1);
                    else f[i][j].set(0, 1);
                    continue;
                }
                //cout << i << " " << j << " " << f[i][j] << endl;
                if(i - 1 > 0) {
                    if(A[i][j] != 0) f[i][j] |= f[i - 1][j] << A[i][j];
                    else f[i][j] |= f[i - 1][j];
                }
                if(j - 1 > 0) {
                    if(A[i][j] != 0) f[i][j] |= f[i][j - 1] << A[i][j];
                    else f[i][j] |= f[i][j - 1];
                }
                //cout << i << " " << j << " " << f[i][j] << endl;
            }
        }
        if(f[n][m].test(aim)) puts("Yes");
        else puts("No");
    }
    return 0;
}

正解

代码的逻辑和上面分析的不太一样，这里是直接用了权值和而不是 1 的数量。但原理是一样的。都是利用了路径构造的特点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e3 + 5;
int A[N][N], f[N][N], g[N][N], n, m;
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) scanf("%d", A[i] + j);
        }
        if((n + m - 1) & 1) {
            puts("No");
            continue;
        }
        for(int i = 1; i <= n; i++) {
            if(i == 1) {
                f[i][1] = g[i][1] = A[i][1];
                for(int j = 2; j <= m; j++) f[i][j] = g[i][j] = f[i][j - 1] + A[i][j];
                continue;
            }
            f[i][1] = f[i - 1][1] + A[i][1];
            g[i][1] = g[i - 1][1] + A[i][1];
            for(int j = 2; j <= m; j++) {
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + A[i][j];
                g[i][j] = min(g[i - 1][j], g[i][j - 1]) + A[i][j];
            }
        }
        if(g[n][m] <= 0 && f[n][m] >= 0) puts("Yes");
        else puts("No");
    }
    return 0;
}

发表于 分类于
本文字数： 433 阅读时长 ≈ 1 分钟

傻逼错误

此处收录了 debug 时发现的一些血压飙升的错误。警钟长鸣。

  1. 注意 n 和 m 的读入顺序和在 for 循环里的使用，别把 n m 弄成 n n。
  2. 小心 1 和 '1'，这是一个情急下很容易写错且难以意识到的问题。
  3. 注意多测的清空，尤其是多测下前向星数组的 head 和 cc。
  4. 注意数组的初始化。特别是 dp 的时候如果懒得写边界特判的时候。
  5. 注意 continue 的位置。如果你只是想跳过中间的某一段代码，后面还有另外的要执行，就不能 continue。这个问题在一开始没有考虑清楚逻辑，后续补上其它代码段时非常容易出现。
  6. 记得删 freopen。
  7. 小心 i*j n*i 之类的东西爆 int。
  8. 线段树大小是 0 的 build 会死循环。小心边界特判。
  9. queue 的初始化非常的慢，空间非常的玄学，不要开大的 queue 数组。

经验

  1. 理清程序逻辑
  2. 看清题目要求（例如昆明那道面积覆盖的矩形，写成了格点覆盖，死活没想到这个问题痛失银牌）
  3. 注意边界特判
  4. 检查傻逼错误（变量名、多测清空、初始化等）
  5. 对于复杂度玄学的 dp，尝试尽可能减少状态比卡常更有效