小乖乖的妙妙屋
0%

CF#808 (Div.1) C. DFS Trees

发表于
本文字数： 3.7k 阅读时长 ≈ 6 分钟

原题链接：https://codeforc.es/contest/1707/problem/C[https://codeforc.es/contest/1707/problem/C]

(家里网络不是很好，最近主站经常上不去，只好上镜像了)

题目大意

给你一个错误的求最小生成树的算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vis := an array of length n
s := a set of edges

function dfs(u):
    vis[u] := true
    iterate through each edge (u, v) in the order from smallest to largest edge weight
        if vis[v] = false
            add edge (u, v) into the set (s)
            dfs(v)

function findMST(u):
    reset all elements of (vis) to false
    reset the edge set (s) to empty
    dfs(u)
    return the edge set (s)

输入一个无重边无自环的联通无向图，且第 \(i\) 条边的边权为 \(i\)。问你调用 findMST(1), findMST(2), ..., findMST(n) 之后，哪些真的找到了 MST。

思路分析

比赛时毫无思路。第二次打 div1，这场的 A 太吓人了，想了老半天，中途一度想润，看到约好一起打的同学已经罚了一发了，只好硬着头皮打下去。结果最后还是掉分了呜呜呜，刚上的橙24小时不到又回去了呜呜呜。

扯歪了，回到这道题上来。

首先，这道题的边权设定，意味着边权两两不同，意味着 MST 有且只有一个。我们可以直接确定出这棵 MST 和不在 MST 里的是哪些边。

这个错误代码的特点是，它用了 DFS。DFS 意味着：访问到一个点后，回溯前，这个点所有的边都会被扫一遍。

因此，我们可以看出第一个问题：

如果边 \((u, v)\) 不在 MST 内，我们假设在 MST 中的边都能正常经过（或者说我们假设不合法边只有这一条）。

那在 DFS 经过 u 之后，必须在回到 u 之前先到达 v。换言之，MST 上必须存在一条不需要经过之前已经经过的点的路径，来从 u 到达 v。

也就是，从满足这个条件：把 v(或 u) 当作 MST 的根时，在 u(或 v) 子树内的点，的点开始 DFS，才可能满足这个要求。其它点必然在回溯到 u 或 v 时走到 (u, v) 这条边。

我们再观察一下 DFS 进行的方式：是从小到大遍历当前点的边。

那有没有可能说，尽管满足了上面的条件，也就是虽然存在一条 MST 上的路径能走到 v，但却选择了 (u, v) 的情形呢？

答案是不可能的，如果先选了 (u, v)，那意味着 MST 内的那条边是更大的。那我们把 MST 内的那条边换成 (u, v)，因为已经知道 u 到 v 有路径连着了，换成 (u, v) 后它依然是个生成树，而且边权和就更小了，这与我们已经确定的 MST 是矛盾的。

综上，我们可以说上面这个条件是一个充分且必要的条件。

换言之，你可以对于每条边求出能不经过这条边的 DFS 起点。最后扫一遍看看哪个点可以不经过任何不合法边就行了。

处理时，我们可以假定一个根，然后我们会看到两种情形：

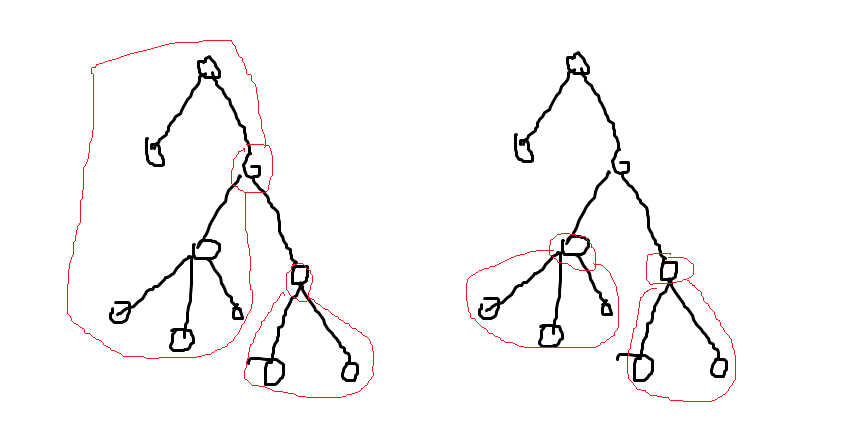
前者，子树互相包含的情况。下面那个点直接取子树，上面的点就是除了子树内包含下面那个点的儿子的那棵子树外，其它的点都可以取。

后者，就是直接取二者的子树了。

用 dfs 序啊树状数组之类的东西搞一下就行了。我用的是链剖。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int N = 1e5 + 5, M = 2e5 + 5;
int n, m, f[N], ex[M][2], ce; // 注意 ex 的大小！
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
int head[N], nex[N << 1], to[N << 1];
inline void addEdge(int u, int v) {
    static int cc = 0;
    nex[++cc] = head[u], head[u] = cc, to[cc] = v;
}
int dfn[N], cnt[N], hson[N], dad[N], topf[N], A[N];
void dfs1(int u, int fa) {
    cnt[u] = 1, dad[u] = fa;
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == fa) continue;
        dfs1(to[i], u);
        cnt[u] += cnt[to[i]];
        if(cnt[to[i]] > cnt[hson[u]]) hson[u] = to[i];
    }
}
void dfs2(int u, int top) {
    static int dn = 0;
    dfn[u] = ++dn, topf[u] = top, A[dn] = u;
    if(hson[u]) dfs2(hson[u], top);
    for(int i = head[u]; i; i = nex[i]) {
        if(to[i] == dad[u] || to[i] == hson[u]) continue;
        dfs2(to[i], to[i]);
    }
}
int mark[N];
inline int lowbit(int x) {
    return x & -x;
}
inline void add(int x, int d) {
    while(x <= n) mark[x] += d, x += lowbit(x);
}
inline int sum(int x) {
    int ans = 0;
    while(x) ans += mark[x], x -= lowbit(x);
    return ans;
}
int main() {
    //freopen("in.txt", "r", stdin);
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) f[i] = i;
    for(int i = 1; i <= m; i++) {
        int u, v, a, b; 
        scanf("%d%d", &u, &v);
        a = find(u), b = find(v);
        if(a != b) {
            addEdge(u, v), addEdge(v, u);
            f[a] = b;
        } else {
            ex[++ce][0] = u, ex[ce][1] = v;
        }
    }
    dfs1(1, 0);
    dfs2(1, 1);
    for(int i = 1; i <= ce; i++) {
        int u = ex[i][0], v = ex[i][1];
        if(dfn[v] + cnt[v] > dfn[u] && dfn[u] > dfn[v]) swap(u, v);
        if(dfn[u] + cnt[u] > dfn[v] && dfn[v] > dfn[u]) {
            add(dfn[v], 1), add(dfn[v] + cnt[v], -1); add(1, 1);
            while(dad[v] != u) {
                if(topf[v] == topf[u]) v = A[dfn[u] + 1];
                else if(dad[topf[v]] == u) v = topf[v];
                else v = dad[topf[v]];
            }
            add(dfn[v], -1), add(dfn[v] + cnt[v], 1);
        } else {
            add(dfn[v], 1), add(dfn[v] + cnt[v], -1);
            add(dfn[u], 1), add(dfn[u] + cnt[u], -1);
        }
    }
    /*for(int i = 1; i <= n; i++) {
        printf("%d %d %d %d %d %d\n", dfn[i], sum(dfn[i]), A[dfn[i]], cnt[i], topf[i], dad[i]);
    }*/
    for(int i = 1; i <= n; i++) {
        if(sum(dfn[i]) == m - n + 1) printf("1");
        else printf("0");
    }
    puts("");
    return 0;
}