原题链接:https://codeforces.com/contest/1695/problem/C
题目大意
给你一个 n * m 的矩阵 (n, m < 1001)。每个元素都是 1 或
-1。你每次只能往下或往右,问你能否找到一条路径使得路上的权值和为
0。
思路分析
比赛的时候只想到了
的做法。
首先,很显然的,步数是 n + m - 1。如果这是个奇数,无解。
然后,转换模型,权值和为 0,其实就是要有一半踩到 1。所以,用一个 n
位的二进制数 f[i][j] 表示从 (1, 1) 走到 (i, j),手上的 1
可能是多少个。于是可以得到这样的 dp 方程:
1
2
| if(A[i][j] == 1) f[i][j] = (f[i - 1][j] << 1) | (f[i][j - 1] << 1);
else f[i][j] = f[i - 1][j] | f[i][j - 1];
|
套上 bitset,可以通过此题。
但这个不是正解。我们仔细想一想,如果 (i, j) 处最多有 b 个 1,最少有 a
个 1。那么是不是意味着 [a, b] 以内的所有值都能在 (i, j) 找到呢?
我们可以感性的这样想:对于任意一条从左上角到右下角的路径,我们一定能找到另一条路径,使得这两条路径只有一个格子不一样。换句话说,通过挪动路径上的某个格子,你可以得到另外一条路径;任意两条路径间一定可以通过若干次的单格子变化得到。
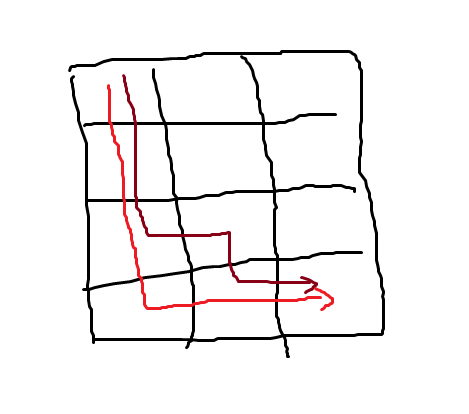
而我们知道,每次只变化一个格子,那就意味着这条路径上 1 的变化量要么是
0 要么是 1。
因此,如果存在 a 个 1 的路径和 b 个 1 的路径,那么我们一定能够凑出 a
到 b 间的所有数目。
代码
bitset
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include <cstdio>
#include <algorithm>
#include <bitset>
#include <iostream>
using namespace std;
const int N = 1e3 + 5;
int n, m, A[N][N];
bitset<N> f[N][N];
int main() {
int T; scanf("%d", &T);
while(T--) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) {
scanf("%d", A[i] + j);
if(A[i][j] == -1) A[i][j] = 0;
f[i][j].reset();
}
if((n + m - 1) & 1) {
puts("No");
continue;
}
int aim = (n + m - 1) / 2;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
if(i == 1 && j == 1) {
if(A[1][1]) f[i][j].set(1, 1);
else f[i][j].set(0, 1);
continue;
}
if(i - 1 > 0) {
if(A[i][j] != 0) f[i][j] |= f[i - 1][j] << A[i][j];
else f[i][j] |= f[i - 1][j];
}
if(j - 1 > 0) {
if(A[i][j] != 0) f[i][j] |= f[i][j - 1] << A[i][j];
else f[i][j] |= f[i][j - 1];
}
}
}
if(f[n][m].test(aim)) puts("Yes");
else puts("No");
}
return 0;
}
|
正解
代码的逻辑和上面分析的不太一样,这里是直接用了权值和而不是 1
的数量。但原理是一样的。都是利用了路径构造的特点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e3 + 5;
int A[N][N], f[N][N], g[N][N], n, m;
int main() {
int T; scanf("%d", &T);
while(T--) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) scanf("%d", A[i] + j);
}
if((n + m - 1) & 1) {
puts("No");
continue;
}
for(int i = 1; i <= n; i++) {
if(i == 1) {
f[i][1] = g[i][1] = A[i][1];
for(int j = 2; j <= m; j++) f[i][j] = g[i][j] = f[i][j - 1] + A[i][j];
continue;
}
f[i][1] = f[i - 1][1] + A[i][1];
g[i][1] = g[i - 1][1] + A[i][1];
for(int j = 2; j <= m; j++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + A[i][j];
g[i][j] = min(g[i - 1][j], g[i][j - 1]) + A[i][j];
}
}
if(g[n][m] <= 0 && f[n][m] >= 0) puts("Yes");
else puts("No");
}
return 0;
}
|
